Decimation in Time
The DFT is defined by
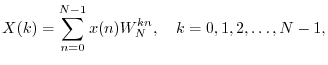
When ![]() is even, the DFT summation can be split into sums over the
odd and even indexes of the input signal:
is even, the DFT summation can be split into sums over the
odd and even indexes of the input signal:
where
Next Section:
Radix 2 FFT
Previous Section:
Coherence Function in Matlab
The DFT is defined by
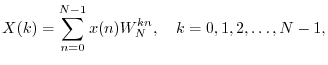
When ![]() is even, the DFT summation can be split into sums over the
odd and even indexes of the input signal:
is even, the DFT summation can be split into sums over the
odd and even indexes of the input signal: