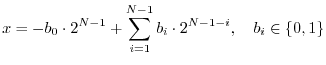Two's-Complement, Integer Fixed-Point Numbers

Let denote the number of bits. Then the value of a two's complement integer fixed-point number can be expressed in terms of its bits $\{b_i\}_{i=0}^{N-1}$ as

$\displaystyle x = - b_0 \cdot 2^{N-1} + \sum_{i=1}^{N - 1} b_i \cdot 2^{N - 1 - i},\quad b_i\in\{0,1\} \protect$

(G.1)

We visualize the binary word containing these bits as

$\displaystyle x = [b_0\, b_1\, \cdots\, b_{N-1}]$

Each bit

is of course either 0 or 1. Check that the

case in Table G.3 is computed correctly using this formula. As an example, the number 3 is expressed as

$\displaystyle 3 =[ 0 1 1 ] = - 0\cdot 4 + 1\cdot 2 + 1 \cdot 1$

while the number -3 is expressed as

$\displaystyle -3 =[ 1 0 1 ] = - 1\cdot 4 + 0\cdot 2 + 1 \cdot 1$

and so on.

The most-significant bit in the word, , can be interpreted as the ``sign bit''. If is ``on'', the number is negative. If it is ``off'', the number is either zero or positive.

The least-significant bit is $b_{N-1}$ . ``Turning on'' that bit adds 1 to the number, and there are no fractions allowed.

The largest positive number is when all bits are on except , in which case $x=2^{N-1}-1$ . The largest (in magnitude) negative number is $10\cdots0$ , i.e., and for all . Table G.4 shows some of the most common cases.