Free Books
   Free Books    Physical Audio Signal Processing  

Circular Disk Rotating in Its Own Plane

For example, the moment of inertia for a uniform circular disk of total mass $ M$ and radius $ R$, rotating in its own plane about a rotation axis piercing its center, is given by

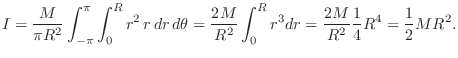
$\displaystyle I = \frac{M}{\pi R^2}\int_{-\pi}^\pi \int_0^R r^2\, r\,dr\,d\thet... ...c{2M}{R^2}\int_0^R r^3 dr = \frac{2M}{R^2}\frac{1}{4} R^4 = \frac{1}{2} M R^2. $

Next Section:
Circular Disk Rotating About Its Diameter
Previous Section:
Whoops, No Angular Momentum!