Convolution Interpretation
Linearly interpolated fractional delay is equivalent to filtering and resampling a weighted impulse train (the input signal samples) with a continuous-time filter having the simple triangular impulse response
Convolution of the weighted impulse train with
This continuous result can then be resampled at the desired fractional delay.
In discrete time processing, the operation Eq.![]() (4.5) can be
approximated arbitrarily closely by digital upsampling by a
large integer factor
(4.5) can be
approximated arbitrarily closely by digital upsampling by a
large integer factor ![]() , delaying by
, delaying by ![]() samples (an integer), then
finally downsampling by
samples (an integer), then
finally downsampling by ![]() , as depicted in Fig.4.7
[96]. The integers
, as depicted in Fig.4.7
[96]. The integers ![]() and
and ![]() are chosen so that
are chosen so that
![]() , where
, where ![]() the desired fractional delay.
the desired fractional delay.
The convolution interpretation of linear interpolation, Lagrange interpolation, and others, is discussed in [407].
Next Section:
Frequency Response of Linear Interpolation
Previous Section:
Minimizing First-Order Allpass Transient Response








![$\displaystyle h_l(t) = \left\{\begin{array}{ll} 1-\left\vert t/T\right\vert, & ...
...ght\vert\leq T, \\ [5pt] 0, & \hbox{otherwise}. \\ \end{array} \right. \protect$](http://www.dsprelated.com/josimages_new/pasp/img959.png)
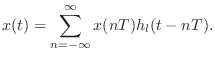
![\includegraphics[width=0.8\twidth]{eps/polyphaseli}](http://www.dsprelated.com/josimages_new/pasp/img963.png)












