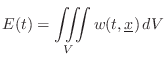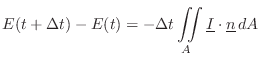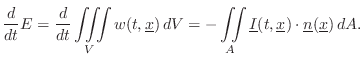Free Books    Physical Audio Signal Processing  

Energy Decay through Lossy Boundaries

Since the acoustic energy density 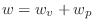$ w=w_v+w_p$ is the energy per unit volume in a 3D sound field, it follows that the total energy of the field is given by integrating over the volume:

$\displaystyle E(t) = \iiint\limits_V w(t,\underline{x}) \,dV $

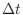
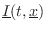
In reverberant rooms and other acoustic systems, the field energy decays over time due to losses. Assuming the losses occur only at the boundary of the volume, we can equate the rate of total-energy change to the rate at which energy exits through the boundaries. 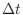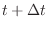In other words, the energy lost by the volume $ V$ in time interval $ \Delta t$ must equal the acoustic intensity $ \underline{I}(t,\underline{x})$ exiting the volume, times $ \Delta t$ (approximating $ I$ as constant between times $ t$ and $ t+\Delta t$):

$\displaystyle E(t+\Delta t) - E(t) = -\Delta t \iint\limits_A \underline{I}\cdot \underline{n}\, dA $

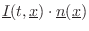
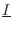
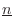
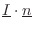
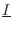
The term $ \underline{I}(t,\underline{x})\cdot\underline{n}(\underline{x})$ is the dot-product of the (vector) intensity $ \underline{I}$ with a unit-vector $ \underline{n}$ chosen to be normal to the surface at position $ \underline{x}$ along the surface. Thus, $ \underline{I}\cdot \underline{n}$ is the component of the acoustic intensity $ \underline{I}$ exiting the volume normal to its surface. 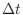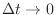(The tangential component does not exit.) Dividing through by $ \Delta t$ and taking a limit as $ \Delta t\to 0$ yields the following conservation law, originally published by Kirchoff in 1867:

$\displaystyle \frac{d}{dt}E = \frac{d}{dt}\iiint\limits_V w(t,\underline{x}) \,... ...imits_A \underline{I}(t,\underline{x})\cdot \underline{n}(\underline{x})\, dA. $

Thus, the rate of change of energy in an ideal acoustic volume $ V$ is equal to the surface integral of the power crossing its boundary. A more detailed derivation appears in [349, p. 37].

Sabine's theory of acoustic energy decay in reverberant room impulse responses can be derived using this conservation relation as a starting point.

Next Section:
Ideal Gas Law
Previous Section:
Acoustic Energy Density