Free Books
   Free Books    Physical Audio Signal Processing  

Energy-Preserving Parameter Changes (Mass-Spring Oscillator)

If the change in $ k$ or $ m$ is deemed to be ``internal'', that is, involving no external interactions, the appropriate accompanying change in the internal state variables is that which conserves energy. For the mass and its velocity, for example, we must have

$\displaystyle \frac{1}{2} m_1 v_1^2 =\frac{1}{2} m_2 v_2^2 $

where $ m_1,m_2$ denote the mass values before and after the change, respectively, and $ v_1,v_2$ denote the corresponding velocities. The velocity must therefore be scaled according to

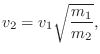
$\displaystyle v_2 = v_1\sqrt{\frac{m_1}{m_2}}, $

since this holds the kinetic energy of the mass constant. Note that the momentum of the mass is changed, however, since

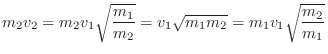
$\displaystyle m_2v_2 = m_2 v_1\sqrt{\frac{m_1}{m_2}} =v_1\sqrt{m_1m_2} =m_1v_1\sqrt{\frac{m_2}{m_1}} $

If the spring constant $ k$ is to change from $ k_1$ to $ k_2$, the instantaneous spring displacement $ x$ must satisfy

$\displaystyle \frac{1}{2} k_1 x_1^2 =\frac{1}{2} k_2 x_2^2 $

In a velocity-wave simulation, displacement is the integral of velocity. Therefore, the energy-conserving velocity correction is impulsive in this case.
Next Section:
Exercises in Wave Digital Modeling
Previous Section:
Mass-Spring Boundedness in Reality