DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Extracting Physical Quantities

Since we are using a force-wave simulation, the state variable $ x(n)$ (delay element output) is in units of physical force (newtons). Specifically, $ x(n) = f^{{+}}(n-1)$. (The physical force is, of course, 0, while its traveling-wave components are not 0 unless the mass is at rest.) Using the fundamental relations relating traveling force and velocity waves

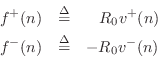
\begin{eqnarray*} f^{{+}}(n) &\isdef & \quad\! R_0 v^{+}(n)\\ f^{{-}}(n) &\isdef & - R_0 v^{-}(n)\\ \end{eqnarray*}

where $ R_0= m$ here, it is easy to convert the state variable $ x(n)$ to other physical units, as we now demonstrate.

The velocity of the mass, for example, is given by

$\displaystyle v(n) = v^{+}(n) + v^{-}(n) = \frac{f^{{+}}(n)}{m} - \frac{f^{{-}}(n)}{m} = \frac{2f^{{+}}(n)}{m} = \frac{2}{m}x(n) $

Thus, the state variable $ x(n)$ can be scaled by $ 2/m$ to ``read out'' the mass velocity.

The kinetic energy of the mass is given by

$\displaystyle {\cal E}_m = \frac{1}{2}mv^2(n) = \frac{2}{m}x^2(n) $

I.e., the square of the state variable $ x(n)$ can be scaled by $ 2/m$ to produce the physical kinetic energy associated with the mass.

Next Section:
A More Formal Derivation of the Wave Digital Force-Driven Mass
Previous Section:
Series Reflection Free Port