Linear Momentum of the Center of Mass
Consider a system of 
point-masses 
, each traveling with
vector velocity
, and not necessarily rigidly attached to
each other. Then the total momentum of the system is
denotes the total mass, and
is the velocity
of the center of mass.
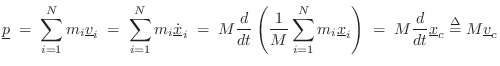
Thus, the momentum
of any collection of masses
(including rigid bodies) equals the total mass 
times the
velocity of the center-of-mass.
Next Section:
Whoops, No Angular Momentum!
Previous Section:
Literature Relevant to Brasses
