DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Pressure is Confined Kinetic Energy

According the kinetic theory of ideal gases [180], air pressure can be defined as the average momentum transfer per unit area per unit time due to molecular collisions between a confined gas and its boundary. Using Newton's second law, this pressure can be shown to be given by one third of the average kinetic energy of molecules in the gas.

$\displaystyle p = \frac{1}{3}\rho \left<u^2\right> $

Here, $ \langle u^2\rangle $ denotes the average squared particle velocity in the gas. (The constant $ 1/3$ comes from the fact that we are interested only in the kinetic energy directed along one dimension in 3D space.)


Proof: This is a classical result from the kinetic theory of gases [180]. Let $ M$ be the total mass of a gas confined to a rectangular volume $ V = Aw$, where $ A$ is the area of one side and $ w$ the distance to the opposite side. Let $ \overline{u}_x$ denote the average molecule velocity in the $ x$ direction. Then the total net molecular momentum in the $ x$ direction is given by $ M\vert\overline{u}_x\vert$. Suppose the momentum $ \overline{u}_x$ is directed against a face of area $ A$. A rigid-wall elastic collision by a mass $ M$ traveling into the wall at velocity $ \overline{u}_x$ imparts a momentum of magnitude $ 2M\overline{u}_x$ to the wall (because the momentum of the mass is changed from $ +M\overline{u}_x$ to $ -M\overline{u}_x$, and momentum is conserved). The average momentum-transfer per unit area is therefore $ 2M\overline{u}_x/A$ at any instant in time. To obtain the definition of pressure, we need only multiply by the average collision rate, which is given by $ \overline{u}_x/(2w)$. That is, the average $ x$-velocity divided by the round-trip distance along the $ x$ dimension gives the collision rate at either wall bounding the $ x$ dimension. Thus, we obtain

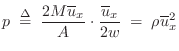
$\displaystyle p \isdefs \frac{2M\overline{u}_x}{A}\cdot \frac{\overline{u}_x}{2w} \eqsp \rho \overline{u}_x^2 $

where $ \rho=M/V$ is the density of the gas in mass per unit volume. The quantity $ \rho\overline{u}_x^2/2$ is the average kinetic energy density of molecules in the gas along the $ x$ dimension. The total kinetic energy density is $ \rho\overline{u}^2/2$, where $ \overline{u}=\sqrt{\overline{u}_x^2+\overline{u}_y^2+\overline{u}_z^2}$ is the average molecular velocity magnitude of the gas. Since the gas pressure must be the same in all directions, by symmetry, we must have $ \overline{u}_x^2=\overline{u}_y^2=\overline{u}_z^2 = \overline{u}^2/3$, so that

$\displaystyle p = \frac{1}{3}\rho \overline{u}^2. $

Next Section:
Bernoulli Equation
Previous Section:
Volume Velocity of a Gas