Area Under a Real Gaussian

Corollary: Setting $p=1/(2\sigma^2)$ in the previous theorem, where $\sigma>0$ is real, we have

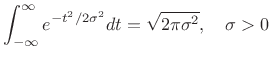$\displaystyle \int_{-\infty}^\infty e^{-t^2/2\sigma^2}dt = \sqrt{2\pi\sigma^2}, \quad \sigma>0$

(D.9)

Therefore, we may normalize the Gaussian to unit area by defining

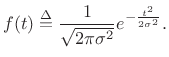$\displaystyle f(t) \isdef \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{t^2}{2\sigma^2}}.$

(D.10)

Since

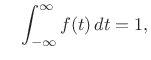$\displaystyle f(t)>0\;\forall t$ and $\displaystyle \quad \int_{-\infty}^\infty f(t)\,dt = 1,$

(D.11)

it satisfies the requirements of a probability density function.

Next Section:
Alternate Proof
Previous Section:
Product of Two Gaussian PDFs

Sign in