Chirplet Frequency-Rate Estimation

The chirp rate $\beta$ may be estimated from the relation $\beta = \alpha c_m/c_p$ as follows:

Let 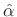${\hat \alpha}$ denote the measured (or known) curvature at the midpoint of the analysis window .
Let and denote weighted averages of the measured curvatures 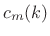and 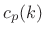along the log-magnitude and phase of a spectral peak, respectively.
Then the chirp-rate $\beta$ estimate may be estimated from the spectral peak by

$\displaystyle \zbox {{\hat \beta}\isdefs {\hat \alpha}\frac{[c_p]}{[c_m]}}$