DTFT of Real Signals

The previous section established that the spectrum of every real signal satisfies

$\displaystyle \hbox{\sc Flip}(X)\eqsp \overline{X}.$

(3.16)

I.e.,

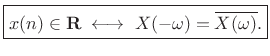$\displaystyle \zbox {x(n)\in{\bf R}\;\longleftrightarrow\;X(-\omega) = \overline{X(\omega)}.}$

(3.17)

In other terms, if a signal

is real, then its spectrum is Hermitian (``conjugate symmetric''). Hermitian spectra have the following equivalent characterizations:

The real part is even, while the imaginary part is odd:

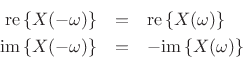
$\begin{eqnarray*} \mbox{re}\left\{X(-\omega)\right\} &=& \mbox{re}\left\{X(\omega)\right\}\\ \mbox{im}\left\{X(-\omega)\right\} &=& -\mbox{im}\left\{X(\omega)\right\} \end{eqnarray*}$
The magnitude is even, while the phase is odd:

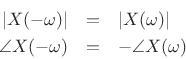
$\begin{eqnarray*} \left\vert X(-\omega)\right\vert &=& \left\vert X(\omega)\right\vert\\ \angle{X(-\omega)} &=& -\angle{X(\omega)} \end{eqnarray*}$

Note that an even function is symmetric about argument zero while an odd function is antisymmetric about argument zero.

Next Section:
Real Even (or Odd) Signals

Sign in