Duration and Bandwidth as Second Moments
More interesting definitions of duration and bandwidth are obtained
using the normalized second moments of the squared magnitude:
where
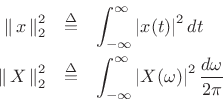
By the DTFT power theorem (§2.3.8), we have
![]() . Note that writing ``
. Note that writing ``
![]() '' and
``
'' and
``
![]() '' is an abuse of notation, but a convenient one.
These duration/bandwidth definitions are routinely used in physics,
e.g., in connection with the Heisenberg uncertainty principle [59].Under these definitions, we have the following theorem
[202, p. 273-274]:
'' is an abuse of notation, but a convenient one.
These duration/bandwidth definitions are routinely used in physics,
e.g., in connection with the Heisenberg uncertainty principle [59].Under these definitions, we have the following theorem
[202, p. 273-274]:
Theorem: If
![]() as
as
![]() , then
, then
with equality if and only if
| (B.63) |
That is, only the Gaussian function (also known as the ``bell curve'' or ``normal curve'') achieves the lower bound on the time-bandwidth product.
Proof: Without loss of generality, we may take consider ![]() to be real
and normalized to have unit
to be real
and normalized to have unit ![]() norm (
norm (
![]() ). From the
Schwarz inequality [264],B.2
). From the
Schwarz inequality [264],B.2
The left-hand side can be evaluated using integration by parts:
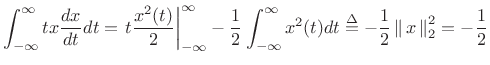 |
(B.65) |
where we used the assumption that
The second term on the right-hand side of (B.65) can be evaluated using the power theorem and differentiation theorem (§B.2):
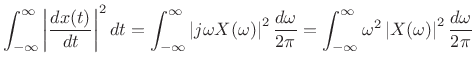 |
(B.66) |
Substituting these evaluations into (B.65) gives
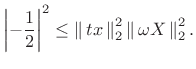 |
(B.67) |
Taking the square root of both sides gives the uncertainty relation sought.
If equality holds in the uncertainty relation (B.63), then (B.65) implies
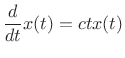 |
(B.68) |
for some constant
Next Section:
Time-Limited Signals
Previous Section:
Geometric Signal Theory








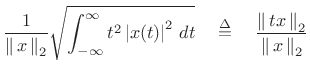
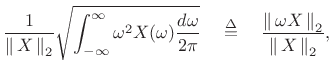
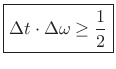
![$\displaystyle \left\vert\int_{-\infty}^\infty t x(t) \left[\frac{d}{dt}x(t)\right] dt\right\vert^2 \leq \int_{-\infty}^\infty t^2 x^2(t) dt \int_{-\infty}^\infty \left\vert\frac{d}{dt}x(t)\right\vert^2 dt. \protect$](http://www.dsprelated.com/josimages_new/sasp2/img2561.png)











