Example: Downsampling by 2
For ![]() , downsampling by 2 can be expressed as
, downsampling by 2 can be expressed as
![]() , so that
(since
, so that
(since
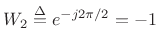 )
)
![\begin{eqnarray*}
Y(z) &=& \frac{1}{2}\left[X\left(W^0_2 z^{1/2}\right) + X\left(W^1_2 z^{1/2}\right)\right] \\ [5pt]
&=& \frac{1}{2}\left[X\left(e^{-j2\pi 0/2} z^{1/2}\right) + X\left(e^{-j2\pi 1/2}z^{1/2}\right)\right] \\ [5pt]
&=& \frac{1}{2}\left[X\left(z^{1/2}\right) + X\left(-z^{1/2}\right)\right] \\ [5pt]
&=& \frac{1}{2}\left[\hbox{\sc Stretch}_2(X) + \hbox{\sc Stretch}_2\left(\hbox{\sc Shift}_\pi(X)\right)\right].
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/sasp2/img1936.png)
Next Section:
Example: Upsampling by 2
Previous Section:
Tightening the IFFTs
For ![]() , downsampling by 2 can be expressed as
, downsampling by 2 can be expressed as
![]() , so that
(since
, so that
(since
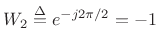 )
)
![\begin{eqnarray*}
Y(z) &=& \frac{1}{2}\left[X\left(W^0_2 z^{1/2}\right) + X\left(W^1_2 z^{1/2}\right)\right] \\ [5pt]
&=& \frac{1}{2}\left[X\left(e^{-j2\pi 0/2} z^{1/2}\right) + X\left(e^{-j2\pi 1/2}z^{1/2}\right)\right] \\ [5pt]
&=& \frac{1}{2}\left[X\left(z^{1/2}\right) + X\left(-z^{1/2}\right)\right] \\ [5pt]
&=& \frac{1}{2}\left[\hbox{\sc Stretch}_2(X) + \hbox{\sc Stretch}_2\left(\hbox{\sc Shift}_\pi(X)\right)\right].
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/sasp2/img1936.png)




