Free Books
   Free Books    Spectral Audio Signal Processing  

Higher Order Moments Revisited


Theorem: The $ n$ th central moment of the Gaussian pdf $ p(x)$ with mean $ \mu$ and variance $ \sigma^2$ is given by

$\displaystyle m_n \isdef {\cal E}_p\{(x-\mu)^n\} = \left\{\begin{array}{ll} (n-1)!!\cdot\sigma^n, & \hbox{$n$\ even} \\ [5pt] $0$, & \hbox{$n$\ odd} \\ \end{array} \right. \protect$ (D.44)

where $ (n-1)!!$ denotes the product of all odd integers up to and including $ n-1$ (see ``double-factorial notation''). Thus, for example, $ m_2=\sigma^2$ , $ m_4=3\,\sigma^4$ , $ m_6=15\,\sigma^6$ , and $ m_8=105\,\sigma^8$ .


Proof: The formula can be derived by successively differentiating the moment-generating function $ M(\alpha) = {\cal E}_p\{\exp(\alpha x)\} = \exp(\mu \alpha + \sigma^2 \alpha^2 / 2)$ with respect to $ \alpha $ and evaluating at $ \alpha=0$ ,D.4 or by differentiating the Gaussian integral

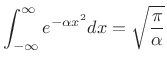$\displaystyle \int_{-\infty}^\infty e^{-\alpha x^2} dx = \sqrt{\frac{\pi}{\alpha}}$ (D.45)

successively with respect to $ \alpha $ [203, p. 147-148]:

\begin{eqnarray*} \int_{-\infty}^\infty (-x^2) e^{-\alpha x^2} dx &=& \sqrt{\pi}(-1/2)\alpha^{-3/2}\\ \int_{-\infty}^\infty (-x^2)(-x^2) e^{-\alpha x^2} + dx &=& \sqrt{\pi}(-1/2)(-3/2)\alpha^{-5/2}\\ \vdots & & \vdots\\ \int_{-\infty}^\infty x^{2k} e^{-\alpha x^2} dx &=& \sqrt{\pi}\,[(2k-1)!!]\,2^{-k/2}\alpha^{-(k+1)/2} \end{eqnarray*}

for $ k=1,2,3,\ldots\,$ . Setting $ \alpha = 1/(2\sigma^2)$ and $ n=2k$ , and dividing both sides by $ \sigma\sqrt{2\pi}$ yields

$\displaystyle {\cal E}_p\{x^n\} \isdefs \frac{1}{\sigma\sqrt{2\pi}}\int_{-\infty}^\infty x^n e^{-\frac{x^2}{2\sigma^2}} dx \eqsp \zbox {\sigma^n \cdot (n-1)!!}$ (D.46)

for $ n=2,4,6,\ldots\,$ . Since the change of variable $ x = \tilde{x}-\mu$ has no affect on the result, (D.44) is also derived for $ \mu\ne0$ .

Next Section:
Moment Theorem
Previous Section:
Gaussian Variance