Free Books
   Free Books    Spectral Audio Signal Processing  

Proof of Aliasing Theorem

To show:

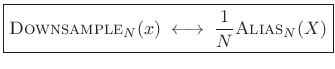
$\displaystyle \zbox {\hbox{\sc Downsample}_N(x) \;\longleftrightarrow\;\frac{1}{N} \hbox{\sc Alias}_N(X)} $

or
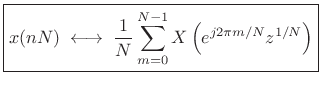
\fbox{$x(nN) \;\longleftrightarrow\;\dfrac{1}{N} \displaystyle\sum_{m=0}^{N-1} X\left(e^{j2\pi m/N} z^{1/N}\right)$}

From the DFT case [264], we know this is true when $ x$ and $ X$ are each complex sequences of length $ N_s$ , in which case $ y$ and $ Y$ are length $ N_s/N$ . Thus,

$\displaystyle x(nN) \;\longleftrightarrow\; Y(\omega_k N) \eqsp \frac{1}{N} \sum_{m=0}^{N-1} X\left(\omega_k + \frac{2\pi}{N} m \right), \; k\in [0,N_s/N)$ (3.38)

where we have chosen to keep frequency samples $ \omega_k$ in terms of the original frequency axis prior to downsampling, i.e., $ \omega_k = 2\pi k/ N_s$ for both $ X$ and $ Y$ . This choice allows us to easily take the limit as $ N_s\to\infty$ by simply replacing $ \omega_k$ by $ \omega$ :

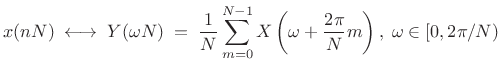$\displaystyle x(nN) \;\longleftrightarrow\; Y(\omega N) \eqsp \frac{1}{N} \sum_{m=0}^{N-1} X\left(\omega + \frac{2\pi}{N} m \right), \; \omega\in[0,2\pi/N)$ (3.39)

Replacing $ \omega$ by $ \omega^\prime =\omega N$ and converting to $ z$ -transform notation $ X(z)$ instead of Fourier transform notation $ X(\omega)$ , with $ z=e^{j\omega^\prime }$ , yields the final result.

Next Section:
Practical Zero Padding
Previous Section:
Real Even (or Odd) Signals