DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Radians versus Cycles

Our usual frequency variable is $ \omega$ in radians per second. However, certain Fourier theorems are undeniably simpler and more elegant when the frequency variable is chosen to be $ f$ in cycles per second. The two are of course related by

$\displaystyle \omega = 2\pi f.$ (B.1)

As an example, $ e^{j\omega t}$ is more compact than $ e^{j2\pi f t}$ . On the other hand, it is nice to get rid of all normalization constants in the Fourier transform and its inverse:
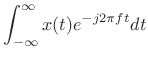$\displaystyle X(f)$ $\displaystyle =$ $\displaystyle \ensuremath{\int_{-\infty}^{\infty}}x(t)e^{-j2\pi f t} dt$ (B.2)
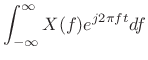$\displaystyle x(t)$ $\displaystyle =$ $\displaystyle \ensuremath{\int_{-\infty}^{\infty}}X(f)e^{j2\pi f t} df$ (B.3)

The ``editorial policy'' for this book is this: Generally, $ \omega$ is preferred, but $ f$ is used when considerable simplification results.

Next Section:
Differentiation Theorem
Previous Section:
Fourier Transform Notation