Sidelobe Specification
Likewise, side-lobe specification can be enforced at frequencies
![]() in the stop-band.
in the stop-band.
| (4.71) |
or
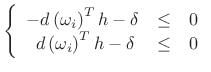 |
(4.72) |
where
| (4.73) |
We need
![$\displaystyle \left[\begin{array}{c}
-d\left(\omega _1\right)^{T}\\
\vdots \\
-d\left(\omega _{K}\right)^{T}\\
d\left(\omega _1\right)^{T}\\
\vdots \\
d\left(\omega _{K}\right)^{T}\end{array}\right]h+\left[\begin{array}{c}
-\delta \\
\vdots \\
-\delta \\
-\delta \\
\vdots \\
-\delta \end{array}\right]$](http://www.dsprelated.com/josimages_new/sasp2/img610.png) |
|||
![$\displaystyle \left[\begin{array}{cc}
-d\left(\omega _1\right)^{T} & -1\\
\vdots & \vdots \\
-d\left(\omega _{K}\right)^{T} & -1\\
d\left(\omega _1\right)^{T} & -1\\
\vdots & \vdots \\
d\left(\omega _{K}\right)^{T} & -1
\end{array}\right]\left[\begin{array}{c}
h\\
\delta \end{array}\right]$](http://www.dsprelated.com/josimages_new/sasp2/img613.png) |
I.e.,
![$\displaystyle \zbox {\mathbf{A}_{sb}\left[\begin{array}{c} h\\ \delta \end{array} \right] \le \mathbf{0}.}$](http://www.dsprelated.com/josimages_new/sasp2/img615.png) |
(4.74) |
Next Section:
LP Standard Form
Previous Section:
DC Constraint
Likewise, side-lobe specification can be enforced at frequencies
![]() in the stop-band.
in the stop-band.
| (4.71) |
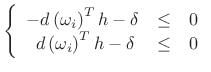 |
(4.72) |
| (4.73) |
![$\displaystyle \left[\begin{array}{c}
-d\left(\omega _1\right)^{T}\\
\vdots \\
-d\left(\omega _{K}\right)^{T}\\
d\left(\omega _1\right)^{T}\\
\vdots \\
d\left(\omega _{K}\right)^{T}\end{array}\right]h+\left[\begin{array}{c}
-\delta \\
\vdots \\
-\delta \\
-\delta \\
\vdots \\
-\delta \end{array}\right]$](http://www.dsprelated.com/josimages_new/sasp2/img610.png) |
|||
![$\displaystyle \left[\begin{array}{cc}
-d\left(\omega _1\right)^{T} & -1\\
\vdots & \vdots \\
-d\left(\omega _{K}\right)^{T} & -1\\
d\left(\omega _1\right)^{T} & -1\\
\vdots & \vdots \\
d\left(\omega _{K}\right)^{T} & -1
\end{array}\right]\left[\begin{array}{c}
h\\
\delta \end{array}\right]$](http://www.dsprelated.com/josimages_new/sasp2/img613.png) |
![$\displaystyle \zbox {\mathbf{A}_{sb}\left[\begin{array}{c} h\\ \delta \end{array} \right] \le \mathbf{0}.}$](http://www.dsprelated.com/josimages_new/sasp2/img615.png) |
(4.74) |