(So far, 79 people got it right out of 228 for a success rate of 34%)
(Thank you to Rick Lyons, author of the top-selling book Understanding Digital Signal Processing, for submitting this Quiz Question.)
This Quiz Question is related to the notion of periodicity. Think about the x(n) time sequence, containing exactly three sinusoidal cycles, defined by
$$ x = \cos (2 \pi f_0 \frac {n}{N} - 6.5 \frac {\pi}{11}) $$shown in Figure 1(a). ($ f_0 = 3 $, $ N = 24 $ and the integer time-domain index $ n $ is $ 0 \leq n \leq N-1 $.)
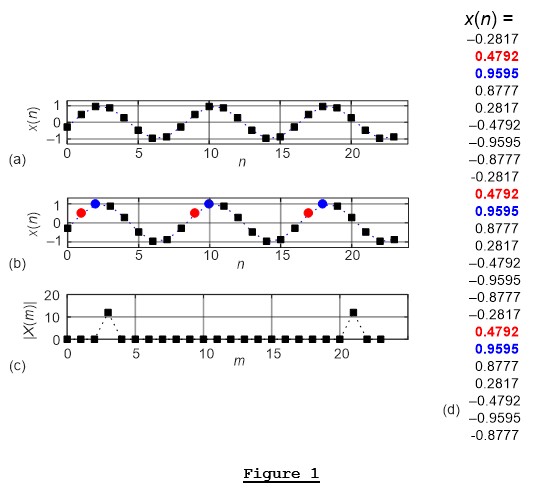
We can call x(n) a "time-domain periodic" sequence meaning it has periodically repeating sample values as shown by the red and blue dots in Figure 1(b) and the x(n) sample values listed in Figure 1(d).
Sequence x(n)'s DFT spectral magnitude samples, |X(m)| having only two non-zero samples, are shown in Figure 1(c).
Quiz Question: Contemplating Figure 1, is it correct to make the following statement:
"All real-valued N-sample sinusoidal sequences containing an integer number of cycles, and having a DFT with only two non-zero spectral components, will be time-domain periodic."
- Comments
- Write a Comment Select to add a comment

It still has period N in the time domain.
Are you referring to the x1(n) sequence given in the answer?
In this case, the time-domain sequences referred to here are only defined for N samples in the time domain. So, they are not "periodic" in the normal sense of the word, since any periodic signal (other than the zero signal) must be infinite in extent.
The meaning of the term "periodic" in this context is defined in the example given just above the question, as a sequence that has:
"periodically repeating sample values"
This seems to be interpreted as no sample values must repeat. Another way to phrase the question would be:
True or False:
"All real-valued N-sample sinusoidal sequences containing an integer number of cycles, and having a DFT with only two non-zero spectral components, will necessarily have repeating sample values."
SPOILER:
Another counterexample would be the 4-sample sequence:
cos(2*pi*n/4+pi/3)
n = 0,...,3.
which is given by:
0.5
-sqrt(3)/2
-0.5
sqrt(3)/2
i.e. just one cycle.

You are correct. The college textbook definition of a "periodic" sequence, of period N, is a sequence that satisfies:
x(n + N) = x(n), for all n.
Your length N = 4 example, cos(2*pi*n/4+pi/3), has a period of P = 4. But to be time-domain periodic (periodically repeating sample values) its period P must less than N. So, indeed, your cos(2*pi*n/4+pi/3) is not time-domain periodic.

Hi Eric. Hope you're doing well.
Please see my below Reply to Micael Collins' Comment.

This definition of periodicity over a finite sequence feels very alien to me. I read the solution and the other comment about this, but I'm still not sure if I grasped the point.
I suspect my mistake was that I looked at the equation used to generate the sequence and noticed that it would repeat periodically if we were to allow n to go off to infinity. But we're not allowed to do that - we just generate a few numbers and those are all we can work with. If we don't get a periodic repetition within those numbers, then we can't say the finite sequence is periodic.
So, if I understand correctly, one period of a sinewave is never "periodic" (regardless of whether it is discrete or continuous). Two periods of a discrete sinewave are only "periodic" if we sample an even number of times. (And so on).
I don't quite see what the value/consequence/meaning of this type of "periodicity" is. It just seems rather coincidental and inconsequential to me. Perhaps I am still missing the point.

Hi Weetabixharry.
I agree with the words in your 3rd paragraph.
As for your 4th paragraph, you're not missing anything. This quizz's topic could be considered a mere curiosity.
To post reply to a comment, click on the 'reply' button attached to each comment. To post a new comment (not a reply to a comment) check out the 'Write a Comment' tab at the top of the comments.
Please login (on the right) if you already have an account on this platform.
Otherwise, please use this form to register (free) an join one of the largest online community for Electrical/Embedded/DSP/FPGA/ML engineers:





















