Kelly-Lochbaum Scattering Junctions
Conservation of energy and mass dictate that, at the impedance
discontinuity, force and velocity variables must be continuous
where velocity is defined as positive to the right on both sides of the junction. Force (or stress or pressure) is a scalar while velocity is a vector with both a magnitude and direction (in this case only left or right). Equations (C.57), (C.58), and (C.59) imply the following scattering equations (a derivation is given in the next section for the more general case of
where
is called the
The scattering equations are illustrated in Figs. C.19b and C.20. In linear predictive coding of speech [482], this structure is called the Kelly-Lochbaum scattering junction, and it is one of several types of scattering junction used to implement lattice and ladder digital filter structures (§C.9.4,[297]).
Next Section:
One-Multiply Scattering Junctions
Previous Section:
Longitudinal Waves in Rods








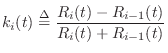
![\includegraphics[scale=0.9]{eps/Fkl}](http://www.dsprelated.com/josimages_new/pasp/img3611.png)












