Amplitude Response
Since the frequency response is a complex-valued function, it has a
magnitude and phase angle for each frequency. The
magnitude of the frequency response is called the amplitude
response (or magnitude frequency response), and it gives the
filter gain at each frequency ![]() .
.
In this example, the amplitude response is
which, for

Figure 3.10a shows a graph of the amplitude response of one case of this filter, obtained by
plotting Eq.![]() (3.5) for
(3.5) for
![]() , and using the
example settings
, and using the
example settings
![]() ,
,
![]() ,
, ![]() , and
, and ![]() .
.
Next Section:
Phase Response
Previous Section:
Frequency Response








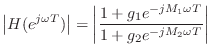
![\includegraphics[width=\twidth]{eps/efr}](http://www.dsprelated.com/josimages_new/filters/img339.png)












