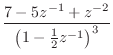Dealing with Repeated Poles Analytically
A pole of multiplicity ![]() has
has
![]() residues associated with it. For example,
residues associated with it. For example,
and the three residues associated with the pole
Let ![]() denote the
denote the ![]() th residue associated with the pole
th residue associated with the pole ![]() ,
,
![]() .
Successively differentiating
.
Successively differentiating
![]()
![]() times with
respect to
times with
respect to ![]() and setting
and setting ![]() isolates the residue
isolates the residue ![]() :
:
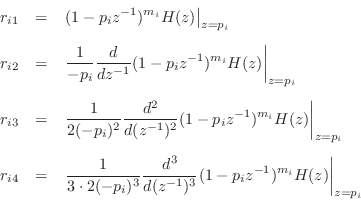
or
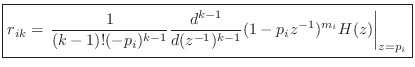
Next Section:
Example
Previous Section:
Example: The General Biquad PFE