Phasor Notation
The complex amplitude
![]() is also defined as the
phasor associated with any sinusoid having amplitude
is also defined as the
phasor associated with any sinusoid having amplitude ![]() and
phase
and
phase ![]() . The term ``phasor'' is more general than ``complex
amplitude'', however, because it also applies to the corresponding
real sinusoid given by the real part of Equations (1.9-1.10).
In other words, the real sinusoids
. The term ``phasor'' is more general than ``complex
amplitude'', however, because it also applies to the corresponding
real sinusoid given by the real part of Equations (1.9-1.10).
In other words, the real sinusoids
![]() and
and
![]() may be expressed as
may be expressed as
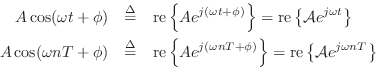
and ![]() is the associated phasor in each case. Thus, we say that
the phasor representation of
is the associated phasor in each case. Thus, we say that
the phasor representation of
![]() is
is
![]() . Phasor analysis is
often used to analyze linear time-invariant systems such as analog
electrical circuits.
. Phasor analysis is
often used to analyze linear time-invariant systems such as analog
electrical circuits.
Next Section:
Plotting Complex Sinusoids as Circular Motion
Previous Section:
Complex Amplitude




















