Free Books    Mathematics of the DFT  

Commutativity of Convolution

Convolution (cyclic or acyclic) is commutative, i.e.,

$\displaystyle \zbox {x\circledast y = y\circledast x .} $


Proof:

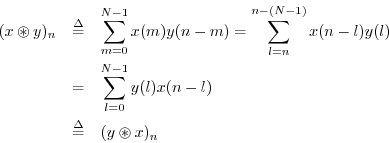
\begin{eqnarray*} (x\circledast y)_n &\isdef & \sum_{m=0}^{N-1}x(m) y(n-m) = \s... ...=& \sum_{l=0}^{N-1}y(l) x(n-l) \\ &\isdef & (y \circledast x)_n \end{eqnarray*}

In the first step we made the change of summation variable $ l\isdeftext n-m$, and in the second step, we made use of the fact that any sum over all $ N$ terms is equivalent to a sum from 0 to $ N-1$.

Next Section:
Convolution as a Filtering Operation
Previous Section:
Examples