Free Books    Mathematics of the DFT  

DFT Definition

The Discrete Fourier Transform (DFT) of a signal $ x$ may be defined by

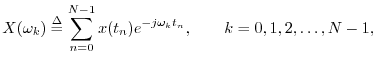
$\displaystyle X(\omega_k ) \isdef \sum_{n=0}^{N-1}x(t_n)e^{-j\omega_k t_n}, \qquad k=0,1,2,\ldots,N-1, $

where ` $ \isdeftext $' means ``is defined as'' or ``equals by definition'', and

\begin{eqnarray*} \sum_{n=0}^{N-1} f(n) &\isdef & f(0) + f(1) + \dots + f(N-1)\\... ...mbox{number of time samples = no.\ frequency samples (integer).} \end{eqnarray*}

The sampling interval $ T$ is also called the sampling period. For a tutorial on sampling continuous-time signals to obtain non-aliased discrete-time signals, see Appendix D.

When all $ N$ signal samples $ x(t_n)$ are real, we say $ x\in{\bf R}^N$. If they may be complex, we write $ x\in{\bf C}^N$. Finally, $ n\in{\bf Z}$ means $ n$ is any integer.

Next Section:
Inverse DFT
Previous Section:
Errata