Free Books    Mathematics of the DFT  

Derivatives of f(x)=a^x

Let's apply the definition of differentiation and see what happens:

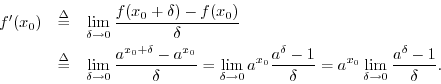
\begin{eqnarray*} f^\prime(x_0) &\isdef & \lim_{\delta\to0} \frac{f(x_0+\delta)-... ...{\delta} = a^{x_0}\lim_{\delta\to0} \frac{a^\delta-1}{\delta}. \end{eqnarray*}

Since the limit of $ (a^\delta-1)/\delta$ as $ \delta\to 0$ is less than 1 for $ a=2$ and greater than $ 1$ for $ a=3$ (as one can show via direct calculations), and since $ (a^\delta-1)/\delta$ is a continuous function of $ a$ for $ \delta>0$, it follows that there exists a positive real number we'll call $ e$ such that for $ a=e$ we get

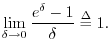
$\displaystyle \lim_{\delta\to 0} \frac{e^\delta-1}{\delta} \isdef 1 . $

For $ a=e$, we thus have $ \left(a^x\right)^\prime = (e^x)^\prime = e^x$.

So far we have proved that the derivative of $ e^x$ is $ e^x$. What about $ a^x$ for other values of $ a$? The trick is to write it as

$\displaystyle a^x = e^{\ln\left(a^x\right)}=e^{x\ln(a)} $

and use the chain rule,3.3 where $ \ln(a)\isdef \log_e(a)$ denotes the log-base-$ e$ of $ a$.3.4 Formally, the chain rule tells us how to differentiate a function of a function as follows:

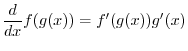
$\displaystyle \frac{d}{dx} f(g(x)) = f^\prime(g(x)) g^\prime(x) $

Evaluated at a particular point $ x_0$, we obtain

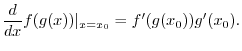
$\displaystyle \frac{d}{dx} f(g(x))\vert _{x=x_0} = f^\prime(g(x_0)) g^\prime(x_0). $

In this case, $ g(x)=x\ln(a)$ so that $ g^\prime(x) = \ln(a)$, and $ f(y)=e^y$ which is its own derivative. The end result is then $ \left(a^x\right)^\prime = \left(e^{x\ln a}\right)^\prime = e^{x\ln(a)}\ln(a) = a^x \ln(a)$, i.e.,

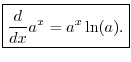
$\displaystyle \zbox {\frac{d}{dx} a^x = a^x \ln(a).} $

Next Section:
Back to e
Previous Section:
Imaginary Exponents