Free Books    Mathematics of the DFT  

Differentiability of Audio Signals

As mentioned in §3.6, every audio signal can be regarded as infinitely differentiable due to the finite bandwidth of human hearing. That is, given any audio signal $ x(t)$, its Fourier transform is given by

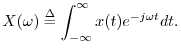
$\displaystyle X(\omega)\isdef \int_{-\infty}^\infty x(t) e^{-j\omega t} dt . $

For the Fourier transform to exist, it is sufficient that $ x(t)$ be absolutely integrable, i.e., $ \int_{-\infty}^\infty\left\vert x(t)\right\vert dt<\infty$. Clearly, all audio signals in practice are absolutely integrable. The inverse Fourier transform is then given by

$\displaystyle x(t) = \frac{1}{2\pi}\int_{-\infty}^\infty X(\omega) e^{j\omega t} d\omega. \protect$

Because hearing is bandlimited to, say, $ 20$ kHz, $ x(t)$ sounds identical to the bandlimited signal

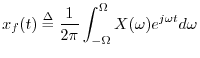
$\displaystyle x_f(t) \isdef \frac{1}{2\pi} \int_{-\Omega}^\Omega X(\omega) e^{j\omega t} d\omega $

where $ \Omega\isdef 2\pi\cdot 20,000$. Now, taking time derivatives is simple (see also §C.1):

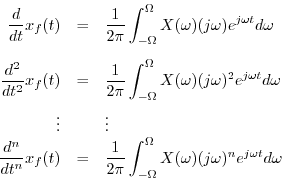
\begin{eqnarray*} \frac{d}{dt} x_f(t) &=& \frac{1}{2\pi} \int_{-\Omega}^\Omega X... ...int_{-\Omega}^\Omega X(\omega) (j\omega)^n e^{j\omega t} d\omega \end{eqnarray*}

Since the length of the integral is finite, there is no possibility that it can ``blow up'' due to the weighting by $ \omega^n$ in the frequency domain introduced by differentiation in the time domain.

A basic Fourier property of signals and their spectra is that a signal cannot be both time limited and frequency limited. Therefore, by conceptually ``lowpass filtering'' every audio signal to reject all frequencies above $ 20$ kHz, we implicitly make every audio signal last forever! Another way of saying this is that the ``ideal lowpass filter `rings' forever''. Such fine points do not concern us in practice, but they are important for fully understanding the underlying theory. Since, in reality, signals can be said to have a true beginning and end, we must admit that all signals we really work with in practice have infinite-bandwidth. That is, when a signal is turned on or off, there is a spectral event extending all the way to infinite frequency (while ``rolling off'' with frequency and having a finite total energy).E.2

In summary, audio signals are perceptually equivalent to bandlimited signals, and bandlimited signals are infinitely smooth in the sense that derivatives of all orders exist at all points time $ t\in(-\infty,\infty)$.

Next Section:
Logarithms
Previous Section:
Points of Infinite Flatness