Free Books    Mathematics of the DFT  

Logarithms

A logarithm $ y=\log_b(x)$ is fundamentally an exponent $ y$ applied to a specific base $ b$ to yield the argument $ x$. That is, $ x = b^y$. The term ``logarithm'' can be abbreviated as ``log''. The base $ b$ is chosen to be a positive real number, and we normally only take logs of positive real numbers $ x>0$ (although it is ok to say that the log of 0 is $ -\infty$). The inverse of a logarithm is called an antilogarithm or antilog; thus, $ x$ is the antilog of $ y$ in the base $ b$.

For any positive number $ x$, we have

$\displaystyle x = b^{\log_b(x)} $

for any valid base $ b>0$. This is just an identity arising from the definition of the logarithm, but it is sometimes useful in manipulating formulas.

When the base is not specified, it is normally assumed to be $ 10$, i.e., $ \log(x) \isdef \log_{10}(x)$. This is the common logarithm.

Base 2 and base $ e$ logarithms have their own special notation:

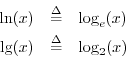
\begin{eqnarray*} \ln(x) &\isdef & \log_e(x) \\ \lg(x) &\isdef & \log_2(x) \end{eqnarray*}

(The use of $ \lg()$ for base $ 2$ logarithms is common in computer science. In mathematics, it may denote a base $ 10$ logarithm.) By far the most common bases are $ 10$, $ e$, and $ 2$. Logs base $ e$ are called natural logarithms. They are ``natural'' in the sense that

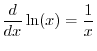
$\displaystyle \frac{d}{dx}\ln(x) = \frac{1}{x} $

while the derivatives of logarithms to other bases are not quite so simple:

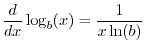
$\displaystyle \frac{d}{dx}\log_b(x) = \frac{1}{x\ln(b)} $

The inverse of the natural logarithm $ y=\ln(x)$ is of course the exponential function $ x=e^y$, and $ e^y$ is its own derivative.

In general, a logarithm $ y$ has an integer part and a fractional part. The integer part is called the characteristic of the logarithm, and the fractional part is called the mantissa. These terms were suggested by Henry Briggs in 1624. ``Mantissa'' is a Latin word meaning ``addition'' or ``make weight''--something added to make up the weight [28].

The following Matlab code illustrates splitting a natural logarithm into its characteristic and mantissa: 

>> x = log(3)
   x = 1.0986
>> characteristic = floor(x)
   characteristic = 1
>> mantissa = x - characteristic
   mantissa = 0.0986

>> % Now do a negative-log example
>> x = log(0.05)
   x = -2.9957
>> characteristic = floor(x)
   characteristic = -3
>> mantissa = x - characteristic
   mantissa = 0.0043

Logarithms were used in the days before computers to perform multiplication of large numbers. Since $ \log(xy) = \log(x)+\log(y)$, one can look up the logs of $ x$ and $ y$ in tables of logarithms, add them together (which is easier than multiplying), and look up the antilog of the result to obtain the product $ xy$. Log tables are still used in modern computing environments to replace expensive multiplies with less-expensive table lookups and additions. This is a classic trade-off between memory (for the log tables) and computation. Nowadays, large numbers are multiplied using FFT fast-convolution techniques.

Changing the Base

By definition, $ x = b^{\log_b(x)}$. Taking the log base $ a$ of both sides gives

$\displaystyle \log_a(x) = \log_b(x) \log_a(b) $

which tells how to convert the base from $ b$ to $ a$, that is, how to convert the log base $ b$ of $ x$ to the log base $ a$ of $ x$. (Just multiply by the log base $ a$ of $ b$.)

Logarithms of Negative and Imaginary Numbers

By Euler's identity, $ e^{j\pi} = -1$, so that

$\displaystyle \ln(-1) = j\pi $

from which it follows that for any $ x<0$, $ \ln(x) = j\pi + \ln(\vert x\vert)$.

Similarly, $ e^{j\pi/2} = j$, so that

$\displaystyle \ln(j) = j\frac{\pi}{2} $

and for any imaginary number $ z = jy$, $ \ln(z) = j\pi/2 + \ln(y)$, where $ y$ is real.

Finally, from the polar representation $ z=r e^{j\theta}$ for complex numbers,

$\displaystyle \ln(z) \isdef \ln(r e^{j\theta}) = \ln(r) + j\theta $

where $ r>0$ and $ \theta$ are real. Thus, the log of the magnitude of a complex number behaves like the log of any positive real number, while the log of its phase term $ e^{j\theta }$ extracts its phase (times $ j$).

Next Section:
Decibels
Previous Section:
Differentiability of Audio Signals