Elementary Relationships
From the above definitions, one can quickly verify
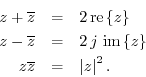
Let's verify the third relationship which states that a complex number multiplied by its conjugate is equal to its magnitude squared:
Next Section:
Euler's Identity
Previous Section:
More Notation and Terminology



















