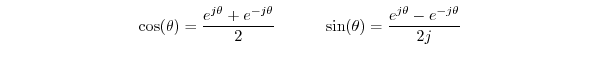Since
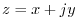 is the algebraic expression of
is the algebraic expression of  in terms of its
rectangular coordinates, the corresponding expression in terms of its polar
coordinates is
in terms of its
rectangular coordinates, the corresponding expression in terms of its polar
coordinates is
There is another, more powerful representation of  in terms of its
polar coordinates. In order to define it, we must introduce Euler's
identity:
in terms of its
polar coordinates. In order to define it, we must introduce Euler's
identity:
 |
(2.5) |
A proof of Euler's identity is given in the next chapter.
Before, the only algebraic representation of a
complex number we had was
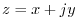
, which fundamentally uses Cartesian (rectilinear) coordinates in
the
complex plane. Euler's identity gives us an alternative
representation in terms of polar coordinates in the complex plane:
We'll call
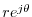
the
polar form of the complex number

, in contrast with the
rectangular form 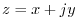
. Polar
form often simplifies algebraic manipulations of complex numbers,
especially when they are multiplied together. Simple rules of
exponents can often be used in place of messier trigonometric
identities. In the case of two complex numbers being multiplied, we
have
A corollary of Euler's identity is obtained by setting
 to get
to get
This has been called the ``most beautiful formula in mathematics'' due
to the extremely simple form in which the fundamental constants
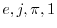
, and 0, together with the elementary operations of addition,
multiplication, exponentiation, and equality, all appear exactly once.
For another example of manipulating the polar form of a complex number,
let's again verify
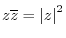 , as we did above in
Eq.
, as we did above in
Eq. (2.4), but this time using polar form:
(2.4), but this time using polar form:
As mentioned in §
2.7, any complex expression can be conjugated
by replacing

by
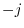
wherever it occurs. This implies

,
as used above. The same result can be obtained by using Euler's
identity to expand
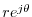
into
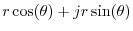
and negating the imaginary part
to obtain
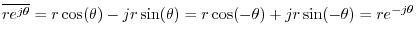
,
where we used also the fact that cosine is an
even function
(

) while sine is
odd
(
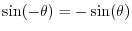
).
We can now easily add a fourth line to that set of examples:
Thus,
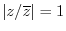
for every
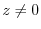
.
Euler's identity can be used to derive formulas for sine and cosine in
terms of
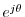 :
:
Similarly,
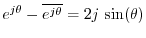 , and
we obtain the following classic identities:
, and
we obtain the following classic identities:
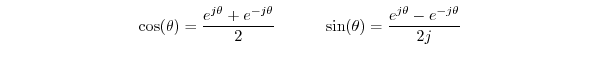
Next Section: De Moivre's TheoremPrevious Section: Elementary Relationships
![]() is the algebraic expression of
is the algebraic expression of ![]() in terms of its
rectangular coordinates, the corresponding expression in terms of its polar
coordinates is
in terms of its
rectangular coordinates, the corresponding expression in terms of its polar
coordinates is
![]() in terms of its
polar coordinates. In order to define it, we must introduce Euler's
identity:
in terms of its
polar coordinates. In order to define it, we must introduce Euler's
identity:
![]() to get
to get
![]() , as we did above in
Eq.
, as we did above in
Eq.![]() (2.4), but this time using polar form:
(2.4), but this time using polar form:
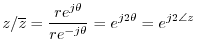
![]() :
:
![\begin{eqnarray*}
e^{j \theta} + \overline{e^{j \theta}}&=&e^{j \theta} + e^{-j ...
...+ \left[\cos(\theta) - j \sin(\theta)\right]\\
&=&2\cos(\theta)
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/mdft/img224.png)
![]() , and
we obtain the following classic identities:
, and
we obtain the following classic identities: