Free Books
   Free Books    Mathematics of the DFT  

Flip Operator

We define the flip operator by

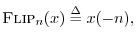$\displaystyle \hbox{\sc Flip}_n(x) \isdef x(-n), \protect$ (7.1)

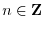
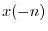
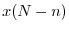
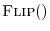
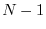
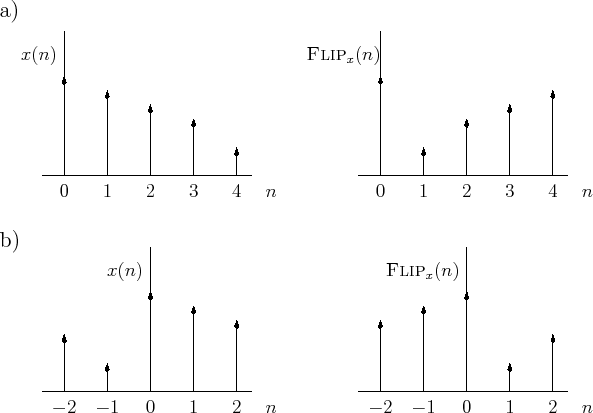
for all sample indices $ n\in{\bf Z}$. By modulo indexing, $ x(-n)$ is the same as $ x(N-n)$. The $ \hbox{\sc Flip}()$ operator reverses the order of samples $ 1$ through $ N-1$ of a sequence, leaving sample 0 alone, as shown in Fig.7.1a. Thanks to modulo indexing, it can also be viewed as ``flipping'' the sequence about the time 0, as shown in Fig.7.1b. 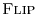The interpretation of Fig.7.1b is usually the one we want, and the $ \hbox{\sc Flip}$ operator is usually thought of as ``time reversal'' when applied to a signal $ x$ or ``frequency reversal'' when applied to a spectrum $ X$.

figure[htbp] \includegraphics{eps/flip}

Next Section:
Shift Operator
Previous Section:
Operator Notation