Free Books
   Free Books    Mathematics of the DFT  

Shift Operator

The shift operator is defined by

$\displaystyle \hbox{\sc Shift}_{\Delta,n}(x) \isdef x(n-\Delta), \quad \Delta\in{\bf Z}, $

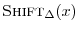
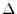
and $ \hbox{\sc Shift}_{\Delta}(x)$ denotes the entire shifted signal. Note that since indexing is modulo $ N$, the shift is circular (or ``cyclic''). However, we normally use it to represent time delay by $ \Delta$ samples. We often use the shift operator in conjunction with zero padding (appending zeros to the signal $ x$, §7.2.7) in order to avoid the ``wrap-around'' associated with a circular shift.

Figure 7.2: Successive one-sample shifts of a sampled periodic sawtooth waveform having first period $ [0,1,2,3,4]$.
\includegraphics[width=\twidth]{eps/shift}

Figure 7.2 illustrates successive one-sample delays of a periodic signal having first period given by $ [0,1,2,3,4]$.

Examples

  • $ \hbox{\sc Shift}_1([1,0,0,0]) = [0,1,0,0]\;$ (an impulse delayed one sample).

  • $ \hbox{\sc Shift}_1([1,2,3,4]) = [4,1,2,3]\;$ (a circular shift example).

  • $ \hbox{\sc Shift}_{-2}([1,0,0,0]) = [0,0,1,0]\;$ (another circular shift example).

Next Section:
Convolution
Previous Section:
Flip Operator