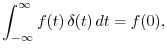Fourier Transform (FT) and Inverse
The Fourier transform of a signal
![]() ,
,
![]() , is defined as
, is defined as
and its inverse is given by
Existence of the Fourier Transform
Conditions for the existence of the Fourier transform are
complicated to state in general [12], but it is sufficient
for ![]() to be absolutely integrable, i.e.,
to be absolutely integrable, i.e.,

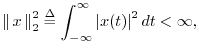
There is never a question of existence, of course, for Fourier transforms of real-world signals encountered in practice. However, idealized signals, such as sinusoids that go on forever in time, do pose normalization difficulties. In practical engineering analysis, these difficulties are resolved using Dirac's ``generalized functions'' such as the impulse (also called the delta function) [38].
The Continuous-Time Impulse
An impulse in continuous time must have ``zero width'' and unit area under it. One definition is
An impulse can be similarly defined as the limit of any integrable pulse shape which maintains unit area and approaches zero width at time 0. As a result, the impulse under every definition has the so-called sifting property under integration,
provided
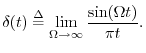
An impulse is not a function in the usual sense, so it is called instead a distribution or generalized function [12,38]. (It is still commonly called a ``delta function'', however, despite the misnomer.)
Next Section:
Fourier Series (FS) and Relation to DFT
Previous Section:
Discrete Time Fourier Transform (DTFT)








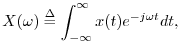

![$\displaystyle \delta(t) \isdef \lim_{\Delta \to 0} \left\{\begin{array}{ll} \fr...
...eq t\leq \Delta \\ [5pt] 0, & \hbox{otherwise}. \\ \end{array} \right. \protect$](http://www.dsprelated.com/josimages_new/mdft/img1700.png)