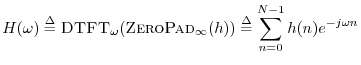DSPRelated.com
Free Books
   Free Books    Mathematics of the DFT  

Frequency Response


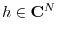Definition: The frequency response of an LTI filter may be defined as the Fourier transform of its impulse response. In particular, for finite, discrete-time signals $ h\in{\bf C}^N$, the sampled frequency response may be defined as

$\displaystyle H(\omega_k) \isdef \hbox{\sc DFT}_k(h). $

The complete (continuous) frequency response is defined using the DTFT (see §B.1), i.e.,

$\displaystyle H(\omega) \isdef \hbox{\sc DTFT}_\omega(\hbox{\sc ZeroPad}_\infty(h)) \isdef \sum_{n=0}^{N-1}h(n) e^{-j\omega n} $

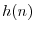
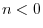
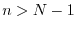
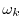
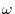
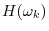
where the summation limits are truncated to $ [0,N-1]$ because $ h(n)$ is zero for $ n<0$ and $ n>N-1$. Thus, the DTFT can be obtained from the DFT by simply replacing $ \omega_k$ by $ \omega$, which corresponds to infinite zero-padding in the time domain. Recall from §7.2.10 that zero-padding in the time domain gives ideal interpolation of the frequency-domain samples $ H(\omega_k)$ (assuming the original DFT included all nonzero samples of $ h$).

Next Section:
Amplitude Response
Previous Section:
Spectrogram of Speech