Free Books    Mathematics of the DFT  

Ideal Spectral Interpolation

Using Fourier theorems, we will be able to show (§7.4.12) that zero padding in the time domain gives exact bandlimited interpolation in the frequency domain.7.9In other words, for truly time-limited signals $ x$, taking the DFT of the entire nonzero portion of $ x$ extended by zeros yields exact interpolation of the complex spectrum--not an approximation (ignoring computational round-off error in the DFT itself). Because the fast Fourier transform (FFT) is so efficient, zero-padding followed by an FFT is a highly practical method for interpolating spectra of finite-duration signals, and is used extensively in practice.

Before we can interpolate a spectrum, we must be clear on what a ``spectrum'' really is. As discussed in Chapter 6, the spectrum of a signal $ x(\cdot)$ at frequency $ \omega$ is defined as a complex number $ X(\omega)$ computed using the inner product

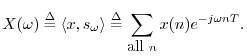
$\displaystyle X(\omega) \isdef \left<x,s_\omega\right> \isdef \sum_{\mbox{all } n} x(n) e^{-j\omega nT}. $

That is, $ X(\omega)$ is the unnormalized coefficient of projection of $ x$ onto the sinusoid $ s_\omega$ at frequency $ \omega$. When $ \omega=\omega_k=2\pi f_s k/N$, for $ k=0,1,\ldots, N-1$, we obtain the special set of spectral samples known as the DFT. For other values of $ \omega$, we obtain spectral points in between the DFT samples. Interpolating DFT samples should give the same result. It is straightforward to show that this ideal form of interpolation is what we call bandlimited interpolation, as discussed further in Appendix D and in Book IV [70] of this series.

Next Section:
Interpolation Operator
Previous Section:
Zero Padding Applications