Free Books
   Free Books    Mathematics of the DFT  

Fundamental Theorem of Algebra

\fbox{\emph{Every $n$th-order polynomial possesses exactly $n$\ complex roots.}}
This is a very powerful algebraic tool.2.4 It says that given any polynomial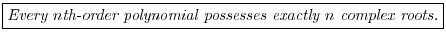

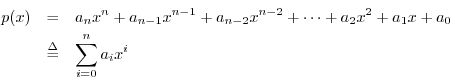
\begin{eqnarray*} p(x) &=& a_n x^n + a_{n-1} x^{n-1} + a_{n-2} x^{n-2} + \cdots + a_2 x^2 + a_1 x + a_0 \\ &\isdef & \sum_{i=0}^n a_i x^i \end{eqnarray*}

we can always rewrite it as

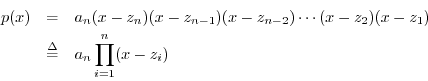
\begin{eqnarray*} p(x) &=& a_n (x - z_n) (x - z_{n-1}) (x - z_{n-2}) \cdots (x - z_2) (x - z_1) \\ &\isdef & a_n \prod_{i=1}^n (x-z_i) \end{eqnarray*}

where the points $ z_i$ are the polynomial roots, and they may be real or complex.

Next Section:
Complex Basics
Previous Section:
Complex Roots