Free Books    Mathematics of the DFT  

Complex Basics

This section introduces various notation and terms associated with complex numbers. As discussed above, complex numbers arise by introducing the square-root of $ -1$ as a primitive new algebraic object among real numbers and manipulating it symbolically as if it were a real number itself:

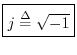
$\displaystyle \zbox {j \isdef \sqrt{-1}} $

Mathematicians and physicists often use $ i$ instead of $ j$ as $ \sqrt{-1}$. The use of $ j$ is common in engineering where $ i$ is more often used for electrical current.

As mentioned above, for any negative number $ c<0$, we have

$\displaystyle \sqrt{c} = \sqrt{(-1)(-c)} = j\sqrt{-c} = j\sqrt{\left\vert c\right\vert}, $

where $ \left\vert c\right\vert$ denotes the absolute value of $ c$. Thus, every square root of a negative number can be expressed as $ j$ times the square root of a positive number.

By definition, we have

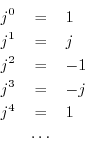
\begin{eqnarray*} j^0 &=& 1 \\ j^1 &=& j \\ j^2 &=& -1 \\ j^3 &=& -j\\ j^4 &=& 1 \\ &\cdots& \end{eqnarray*}

and so on. Thus, the sequence $ x(n)\isdef j^n$, $ n=0,1,2,\ldots$ is a periodic sequence with period $ 4$, since $ j^{n+4}=j^n j^4=j^n$. (We'll learn later that the sequence $ j^n$ is a sampled complex sinusoid having frequency equal to one fourth the sampling rate.)

Every complex number $ z$ can be written as

$\displaystyle \zbox {z = x + j y} $

where $ x$ and $ y$ are real numbers. We call $ x$ the real part and $ y$ the imaginary part. We may also use the notation

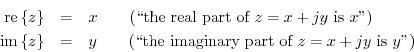
\begin{eqnarray*} \mbox{re}\left\{z\right\} &=& x \qquad \mbox{(\lq\lq the real part ... ...&=& y \qquad \mbox{(\lq\lq the imaginary part of $z=x+jy$\ is $y$'')} \end{eqnarray*}

Note that the real numbers are the subset of the complex numbers having a zero imaginary part ($ y=0$).

The rule for complex multiplication follows directly from the definition of the imaginary unit $ j$:

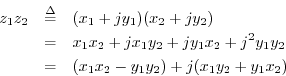
\begin{eqnarray*} z_1 z_2 &\isdef & (x_1 + j y_1) (x_2 + j y_2) \\ &=& x_1 x_2... ...j^2 y_1 y_2 \\ &=& (x_1 x_2 - y_1 y_2) + j (x_1 y_2 + y_1 x_2) \end{eqnarray*}

In some mathematics texts, complex numbers $ z$ are defined as ordered pairs of real numbers $ (x,y)$, and algebraic operations such as multiplication are defined more formally as operations on ordered pairs, e.g., $ (x_1,y_1) \cdot (x_2,y_2) \isdeftext (x_1 x_2 - y_1 y_2, x_1 y_2 + y_1 x_2)$. However, such formality tends to obscure the underlying simplicity of complex numbers as a straightforward extension of real numbers to include $ j\isdeftext \sqrt{-1}$.

It is important to realize that complex numbers can be treated algebraically just like real numbers. That is, they can be added, subtracted, multiplied, divided, etc., using exactly the same rules of algebra (since both real and complex numbers are mathematical fields). It is often preferable to think of complex numbers as being the true and proper setting for algebraic operations, with real numbers being the limited subset for which $ y=0$.

Next Section:
The Complex Plane
Previous Section:
Fundamental Theorem of Algebra