Geometric Series
Recall that for any complex number
![]() , the signal
, the signal
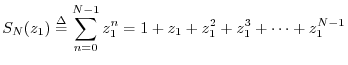
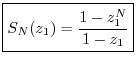
Proof: We have
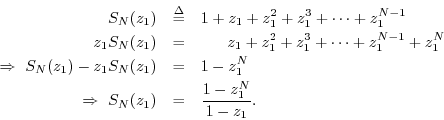
When ![]() ,
, ![]() , by inspection of the definition of
, by inspection of the definition of
![]() .
.
Next Section:
Orthogonality of Sinusoids
Previous Section:
Signal Projection Problems
Recall that for any complex number
![]() , the signal
, the signal
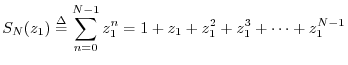
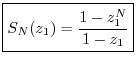
Proof: We have
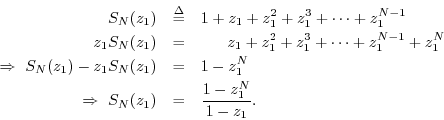
When ![]() ,
, ![]() , by inspection of the definition of
, by inspection of the definition of
![]() .
.