Free Books    Mathematics of the DFT  

Interpolation Operator

The interpolation operator $ \hbox{\sc Interp}_L()$ interpolates a signal by an integer factor $ L$ using bandlimited interpolation. For frequency-domain signals $ X(\omega_k)$, $ k=0,1,2,\ldots,N-1$, we may write spectral interpolation as follows:

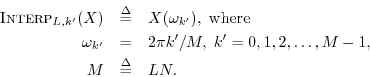
\begin{eqnarray*} \hbox{\sc Interp}_{L,k^\prime }(X) &\isdef & X(\omega_{k^\prim... ...i k^\prime /M,\; k^\prime =0,1,2,\dots,M-1,\;\\ M&\isdef & LN. \end{eqnarray*}

Since $ X(\omega_k )\isdeftext \hbox{\sc DFT}_{N,k}(x)$ is initially only defined over the $ N$ roots of unity in the $ z$ plane, while $ X(\omega_{k^\prime })$ is defined over $ M=LN$ roots of unity, we define $ X(\omega_{k^\prime })$ for $ \omega_{k^\prime }\neq\omega_k $ by ideal bandlimited interpolation (specifically time-limited spectral interpolation in this case).

For time-domain signals $ x(n)$, exact interpolation is similarly bandlimited interpolation, as derived in Appendix D.

Next Section:
Repeat Operator
Previous Section:
Ideal Spectral Interpolation