DSPRelated.com
Free Books
   Free Books    Mathematics of the DFT  

Linear Phase Signals

In practice, a signal may be said to be linear phase when its phase is of the form

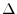
$\displaystyle \Theta(\omega_k)= - \Delta \cdot \omega_k\pm \pi I(\omega_k), $

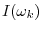
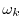
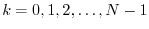
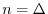
where $ \Delta$ is any real constant (usually an integer), and $ I(\omega_k)$ is an indicator function which takes on the values 0 or $ 1$ over the points $ \omega_k$, $ k=0,1,2,\ldots,N-1$. An important class of examples is when the signal is regarded as a filter impulse response.7.14 What all such signals have in common is that they are symmetric about the time $ n=\Delta$ in the time domain (as we will show on the next page). Thus, the term ``linear phase signal'' often really means ``a signal whose phase is linear between $ \pm\pi$ discontinuities.''

Next Section:
Zero Phase Signals
Previous Section:
Linear Phase Terms