Prime Factor Algorithm
(PFA)
By the prime factorization theorem, every integer  can be uniquely
factored into a product of prime numbers
can be uniquely
factored into a product of prime numbers 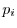 raised to an
integer power
raised to an
integer power 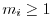 :
:
As discussed above, a mixed-radix
Cooley Tukey FFT can be used to
implement a length
 DFT
DFT using DFTs of length
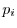
. However, for
factors of

that are mutually prime (such as
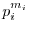
and
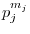
for

), a more efficient
prime factor
algorithm (PFA), also called the
Good-Thomas FFT algorithm,
can be used [
26,
80,
35,
43,
10,
83].
A.4
The
Chinese Remainder
Theorem
is used to
re-index either the input or output samples for the PFA.
A.5Since the PFA is only applicable to mutually prime factors of

, it
is ideally combined with a mixed-radix Cooley-Tukey FFT, which works
for any integer factors.
It is interesting to note that the PFA actually predates the
Cooley-Tukey FFT paper of 1965 [16], with Good's
1958 work on the PFA being cited in that paper [83].
The PFA and Winograd transform [43] are
closely related, with the PFA being somewhat faster [9].
Next Section: Rader's FFT Algorithm for Prime LengthsPrevious Section: Mixed-Radix Cooley-Tukey FFT
![]() can be uniquely
factored into a product of prime numbers
can be uniquely
factored into a product of prime numbers ![]() raised to an
integer power
raised to an
integer power ![]() :
:




















