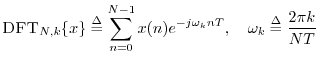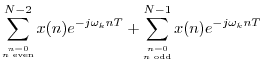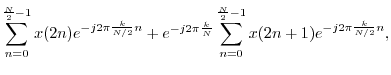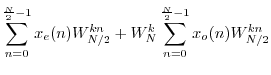Mixed-Radix Cooley-Tukey FFT

When the desired DFT length can be expressed as a product of smaller integers, the Cooley-Tukey decomposition provides what is called a mixed radix Cooley-Tukey FFT algorithm.^A.2

Two basic varieties of Cooley-Tukey FFT are decimation in time (DIT) and its Fourier dual, decimation in frequency (DIF). The next section illustrates decimation in time.

Decimation in Time

The DFT is defined by

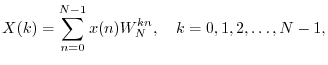
$\displaystyle X(k) = \sum_{n=0}^{N-1} x(n) W_N^{kn}, \quad k=0,1,2,\ldots,N-1,$

where

is the input signal amplitude at time

, and

$\displaystyle W_N \isdef e^{-j\frac{2\pi}{N}}.\quad \hbox{(primitive $N$th root of unity)}$

Note that

When is even, the DFT summation can be split into sums over the odd and even indexes of the input signal:

$\displaystyle X(\omega_k)$	$\displaystyle \isdef$	$\displaystyle \hbox{\sc DFT}_{{N,k}}\{x\} \isdef \sum_{n=0}^{N-1} x(n) e^{-j\omega_k n T}, \quad \omega_k \isdef \frac{2\pi k}{NT}$
	$\displaystyle =$	$\displaystyle \sum_{{\stackrel{n=0}{\vspace{2pt}\mbox{\tiny$n$\ even}}}}^{N-2} ... ...stackrel{n=0}{\vspace{2pt}\mbox{\tiny$n$\ odd}}}}^{N-1} x(n) e^{-j\omega_k n T}$
	$\displaystyle =$	$\displaystyle \sum_{n=0}^{\frac{N}{2}-1} x(2n) e^{-j2\pi \frac{k}{N/2} n} + e^{-j2\pi\frac{k}{N}}\sum_{n=0}^{\frac{N}{2}-1} x(2n+1) e^{-j2\pi \frac{k}{N/2} n},$
	$\displaystyle =$	$\displaystyle \sum_{n=0}^{\frac{N}{2}-1} x_e(n) W_{N/2}^{kn} + W_N^k \sum_{n=0}^{\frac{N}{2}-1} x_o(n) W_{N/2}^{kn}$
	$\displaystyle \isdef$	$\displaystyle \hbox{\sc DFT}_{{\frac{N}{2},k}}\{\hbox{\sc Downsample}_2(x)\}$
		$\displaystyle \mathop{\quad} +\;W_N^k\cdot\hbox{\sc DFT}_{{\frac{N}{2},k}}\{\hbox{\sc Downsample}_2[\hbox{\sc Shift}_1(x)]\}, \protect$	(A.1)

where $x_e(n)\isdef x(2n)$ and $x_o(n)\isdef x(2n+1)$ denote the even- and odd-indexed samples from

. Thus, the length

DFT is computable using two length

DFTs. The complex factors $W_N^k=e^{-j\omega_k}=\exp(-j2\pi k/N)$ are called twiddle factors. The splitting into sums over even and odd time indexes is called decimation in time. (For decimation in frequency, the inverse DFT of the spectrum $X(\omega_k)$ is split into sums over even and odd bin numbers

Radix 2 FFT

When is a power of , say where is an integer, then the above DIT decomposition can be performed times, until each DFT is length . A length DFT requires no multiplies. The overall result is called a radix 2 FFT. A different radix 2 FFT is derived by performing decimation in frequency.

A split radix FFT is theoretically more efficient than a pure radix 2 algorithm [73,31] because it minimizes real arithmetic operations. The term ``split radix'' refers to a DIT decomposition that combines portions of one radix 2 and two radix 4 FFTs [22].^A.3On modern general-purpose processors, however, computation time is often not minimized by minimizing the arithmetic operation count (see §A.7 below).

Radix 2 FFT Complexity is N Log N

Putting together the length DFT from the length- DFTs in a radix-2 FFT, the only multiplies needed are those used to combine two small DFTs to make a DFT twice as long, as in Eq. $\,$ (A.1). Since there are approximately (complex) multiplies needed for each stage of the DIT decomposition, and only $\lg N$ stages of DIT (where $\lg N$ denotes the log-base-2 of ), we see that the total number of multiplies for a length DFT is reduced from ${\cal O}(N^2)$ to ${\cal O}(N\lg N)$ , where ${\cal O}(x)$ means ``on the order of ''. More precisely, a complexity of ${\cal O}(N\lg N)$ means that given any implementation of a length- radix-2 FFT, there exist a constant and integer such that the computational complexity ${\cal C}(N)$ satisfies

$\displaystyle {\cal C}(N) \leq C N \lg N$

for all

. In summary, the complexity of the radix-2 FFT is said to be ``N log N'', or ${\cal O}(N\lg N)$ .

Fixed-Point FFTs and NFFTs

Recall (e.g., from Eq. $\,$ (6.1)) that the inverse DFT requires a division by that the forward DFT does not. In fixed-point arithmetic (Appendix G), and when is a power of 2, dividing by may be carried out by right-shifting $\log_2(N)$ places in the binary word. Fixed-point implementations of the inverse Fast Fourier Transforms (FFT) (Appendix A) typically right-shift one place after each Butterfly stage. However, superior overall numerical performance may be obtained by right-shifting after every other butterfly stage [8], which corresponds to dividing both the forward and inverse FFT by $\sqrt{N}$ (i.e., $\sqrt{N}$ is implemented by half as many right shifts as dividing by ). Thus, in fixed-point, numerical performance can be improved, no extra work is required, and the normalization work (right-shifting) is spread equally between the forward and reverse transform, instead of concentrating all right-shifts in the inverse transform. The NDFT is therefore quite attractive for fixed-point implementations.

Because signal amplitude can grow by a factor of 2 from one butterfly stage to the next, an extra guard bit is needed for each pair of subsequent NDFT butterfly stages. Also note that if the DFT length is not a power of , the number of right-shifts in the forward and reverse transform must differ by one (because $K=\log_2(N)$ is odd instead of even).