Free Books
   Free Books    Mathematics of the DFT  

Projection onto Linearly Dependent Vectors

Now consider another example:

\begin{eqnarray*} \sv_0 &\isdef & [1,1], \\ \sv_1 &\isdef & [-1,-1]. \end{eqnarray*}

The projections of $ x=[x_0,x_1]$ onto these vectors are

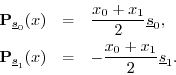
\begin{eqnarray*} {\bf P}_{\sv_0}(x) &=& \frac{x_0 + x_1}{2}\sv_0, \\ {\bf P}_{\sv_1}(x) &=& -\frac{x_0 + x_1}{2}\sv_1. \end{eqnarray*}

The sum of the projections is

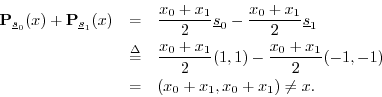
\begin{eqnarray*} {\bf P}_{\sv_0}(x) + {\bf P}_{\sv_1}(x) &=& \frac{x_0 + x_1}... ... + x_1}{2} (-1,-1) \\ &=& \left(x_0+x_1,x_0+x_1\right) \neq x. \end{eqnarray*}

Something went wrong, but what? It turns out that a set of $ N$ vectors can be used to reconstruct an arbitrary vector in $ {\bf C}^N$ from its projections only if they are linearly independent. In general, a set of vectors is linearly independent if none of them can be expressed as a linear combination of the others in the set. What this means intuitively is that they must ``point in different directions'' in $ N$-space. In this example $ s_1 = - s_0$ so that they lie along the same line in $ 2$-space. As a result, they are linearly dependent: one is a linear combination of the other ( $ s_1 = (-1)s_0$).

Next Section:
Projection onto Non-Orthogonal Vectors
Previous Section:
Changing Coordinates