Properties of DB Scales
In every kind of dB, a factor of 10 in amplitude increase corresponds to a 20 dB boost (increase by 20 dB):
, of course. A function 
which is
proportional to 
is said to ``fall off'' (or ``roll off'') at the
rate of 
dB per decade. That is, for every factor of 
in 
(every ``decade''), the amplitude drops dB.
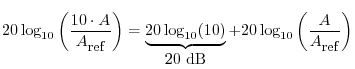
Similarly, a factor of 2 in amplitude gain corresponds to a 6 dB boost:
dB
which is proportional to is said to fall off
dB per octave. That is, for every factor of 
in
(every ``octave''), the amplitude drops close to dB. Thus, 6 dB
per octave is the same thing as 20 dB per decade.
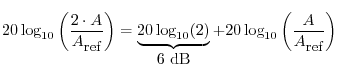
A doubling of power corresponds to a 3 dB boost:
dB
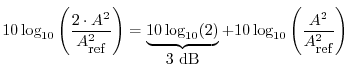
Finally, note that the choice of reference merely determines a vertical offset in the dB scale:
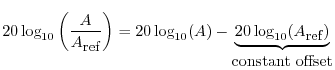
Next Section:
Specific DB Scales
Previous Section:
Logarithms of Negative and Imaginary Numbers
