Specific DB Scales

Since we so often rescale our signals to suit various needs (avoiding overflow, reducing quantization noise, making a nicer plot, etc.), there seems to be little point in worrying about what the dB reference is--we simply choose it implicitly when we rescale to obtain signal values in the range we want to see. In particular, dB relative to full scale ( $20\log_{10}(A/A_{\mbox{\small max}})$ ), abbreviated dBFS, is perhaps the most commonly used case in the digital audio world. Thus, 0 dBFS means maximum amplitude, and typical amplitude levels are negative in dBFS. In addition, there are a few specific dB scales that are worth knowing about.

DBm Scale

One common dB scale in audio recording is the dBm scale in which the reference power is taken to be a milliwatt (1 mW) dissipated by a 600 Ohm resistor. (See §F.3 for a primer on resistors, voltage, current, and power.)

DBV Scale

Another dB scale is the dBV scale which sets 0 dBV to 1 volt. Thus, a 100-volt signal is

$\displaystyle 20\log_{10}\left(\frac{100V}{1V}\right) =$ 40 dBV

and a 1000-volt signal is

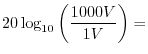$\displaystyle 20\log_{10}\left(\frac{1000V}{1V}\right) =$ 60 dBV

Note that the dBV scale is undefined for current or power, unless the voltage is assumed to be across a standard resistor value, such as 600 Ohms.

DB SPL

Sound Pressure Level (SPL) is defined using a reference which is approximately the intensity of 1000 Hz sinusoid that is just barely audible (zero ``phons''). In pressure units:^F.3

$\begin{eqnarray*} \mbox{$0$\ dB SPL} &\isdef & \mbox{0.0002 $\mu$bar (micro-baro... ...c{\mbox{\small nt}}{\mbox{\small m}^2} \quad\mbox{(MKS units)} \end{eqnarray*}$

In intensity units:

$\displaystyle I_0 = 10^{-16} \frac{\mbox{\small W}}{\mbox{\small cm}^2}$

which corresponds to a root-mean-square (rms) pressure amplitude of

$\mu$ Pa, or about

$\mu$ Pa, as listed above. The wave impedance of air plays the role of ``resistor'' in relating the pressure- and intensity-based references exactly analogous to the dBm case discussed above.

Since sound is created by a time-varying pressure, we compute sound levels in dB-SPL by using the average intensity (averaged over at least one period of the lowest frequency contained in the sound).

Table F.1 gives a list of common sound levels and their dB equivalents [54]:

Table F.1: Approximate dB-SPL level of common sounds. (Information from S. S. Stevens, F. Warshofsky, and the Editors of Time-Life Books, Sound and Hearing, Life Science Library, Time-Life Books, Alexandria, VA, 1965, p. 173.)

Sound	dB-SPL
Jet engine at 3m	140
Threshold of pain	130
Rock concert	120
Accelerating motorcycle at 5m	110
Pneumatic hammer at 2m	100
Noisy factory	90
Vacuum cleaner	80
Busy traffic	70
Quiet restaurant	50
Residential area at night	40
Empty movie house	30
Rustling of leaves	20
Human breathing (at 3m)	10
Threshold of hearing (good ears)	0

In my experience, the ``threshold of pain'' is most often defined as 120 dB.

The relationship between sound amplitude and actual loudness is complex [76]. Loudness is a perceptual dimension while sound amplitude is physical. Since loudness sensitivity is closer to logarithmic than linear in amplitude (especially at moderate to high loudnesses), we typically use decibels to represent sound amplitude, especially in spectral displays.

The sone amplitude scale is defined in terms of actual loudness perception experiments [76]. At 1kHz and above, loudness perception is approximately logarithmic above 50 dB SPL or so. Below that, it tends toward being more linear.

The phon amplitude scale is simply the dB scale at 1kHz [76, p. 111]. At other frequencies, the amplitude in phons is defined by following the equal-loudness curve over to 1 kHz and reading off the level there in dB SPL. In other words, all pure tones have the same loudness at the same phon level, and 1 kHz is used to set the reference in dB SPL. Just remember that one phon is one dB-SPL at 1 kHz. Looking at the Fletcher-Munson equal-loudness curves [76, p. 124], loudness in phons can be read off along the vertical line at 1 kHz.

Classically, the intensity level of a sound wave is its dB SPL level, measuring the peak time-domain pressure-wave amplitude relative to $10^{-16}$ watts per centimeter squared (i.e., there is no consideration of the frequency domain here at all).

Another classical term still encountered is the sensation level of pure tones: The sensation level is the number of dB SPL above the hearing threshold at that frequency [76, p. 110].

For further information on ``doing it right,'' see, for example,
http://www.measure.demon.co.uk/Acoustics_Software/loudness.html.

DBA (A-Weighted DB)

The so-called A-weighted dB scale (abbreviated dBA) is based on the Fletcher-Munson equal-loudness curve for an SPL of 40 phons.^F.4 Thus, a dBA weighting assumes a fairly quiet pure tone. Despite this assumption, the dBA weighting is often used as an approximate equal loudness adjustment for measured spectra.

An analog filter transfer function that can be used to implement an approximate A-weighting is given by^F.5

$\displaystyle H_A(s) = \frac{k_A \cdot s^4}{(s+129.4)^2 (s+676.7) (s+4636) (s+76655)^2}$

where $k_A \approx 7.39705\times 10^9$ normalizes the gain to unity at 1 kHz.

The ITU-R 468 noise weighting^F.6is said to perform better for measuring noise in audio systems.

DB for Display

In practical signal processing, it is common to choose the maximum signal magnitude as the reference amplitude. That is, we normalize the signal so that the maximum amplitude is defined as 1, or 0 dB. This convention is also used by ``sound level meters'' in audio recording. When displaying magnitude spectra, the highest spectral peak is often normalized to 0 dB. We can then easily read off lower peaks as so many dB below the highest peak.

Figure F.1b shows a plot of the Fast Fourier Transform (FFT) of ten periods of a ``Kaiser-windowed'' sinusoid at Hz. (FFT windows are introduced in §8.1.4. The window is used to taper a finite-duration section of the signal.) Note that the peak dB magnitude has been normalized to zero, and that the plot has been clipped at -100 dB.

**Figure F.1:** Windowed sinusoid (top) and its FFT magnitude (bottom).
$\includegraphics[width=\twidth]{eps/freqdpy}$

Below is the Matlab code for producing Fig.F.1. Note that it contains several elements (windows, zero padding, spectral interpolation) that we will not cover until later. They are included here as ``forward references'' in order to keep the example realistic and practical, and to give you an idea of ``how far we have to go'' before we know how to do practical spectrum analysis. Otherwise, the example just illustrates plotting spectra on an arbitrary dB scale between convenient limits.

% Practical display of the fft of a synthesized sinusoid

fs = 44100;             % Sampling rate
f = 440;                % Sinusoidal frequency = A-440
nper = 10;              % Number of periods to synthesize
dur = nper/f;           % Duration in seconds
T = 1/fs;               % Sampling period
t = 0:T:dur;            % Discrete-time axis in seconds
L = length(t)           % Number of samples to synthesize
ZP = 5;                 % Zero padding factor
N = 2^(nextpow2(L*ZP))  % FFT size (power of 2)

x = cos(2*pi*f*t);      % A sinusoid at A-440 ("row vector")
w = kaiser(L,8);        % An "FFT window"
xw = x .* w';           % Need to transpose w to get a row
sound(xw,fs);           % Might as well listen to it
xzp = [xw,zeros(1,N-L)];% Zero-padded FFT input buffer
X = fft(xzp);           % Interpolated spectrum of xw

Xmag = abs(X);          % Spectral magnitude
Xdb = 20*log10(Xmag);   % Spectral magnitude in dB

XdbMax = max(Xdb);      % Peak dB magnitude
Xdbn = Xdb - XdbMax;    % Normalize to 0dB peak

dBmin = -100;           % Don't show anything lower than this
Xdbp = max(Xdbn,dBmin); % Normalized, clipped, dB mag spec
fmaxp = 2*f;            % Upper frequency limit of plot, Hz
kmaxp = fmaxp*N/fs;     % Upper frequency limit of plot, bins
fp = fs*[0:kmaxp]/N;    % Frequency axis in Hz

% Ok, plot it already!

subplot(2,1,1);
plot(1000*t,xw);
xlabel('Time (ms)');
ylabel('Amplitude');
title(sprintf(['a) %d Periods of a %3.0f Hz Sinusoid, ',
               'Kaiser Windowed'],nper,f)R);

subplot(2,1,2);
plot(fp,Xdbp(1:kmaxp+1)); grid;
% Plot a dashed line where the peak should be:
  hold on; plot([440 440],[dBmin,0],'--'); hold off;
xlabel('Frequency (Hz)');
ylabel('Magnitude (dB)');
title(sprintf(['b) Interpolated FFT of %d Periods of ',...
        '%3.0f Hz Sinusoid'],nper,f));

The following more compact Matlab produces essentially the same plot, but without the nice physical units on the horizontal axes:

x = cos([0:2*pi/20:10*2*pi]); % 10 periods, 20 samples/cycle
L = length(x);
xw = x' .* kaiser(L,8);
N = 2^nextpow2(L*5);
X = fft([xw',zeros(1,N-L)]);

subplot(2,1,1); plot(xw);
xlabel('Time (samples)'); ylabel('Amplitude');
title('a) 10 Periods of a Kaiser-Windowed Sinusoid');

subplot(2,1,2); kmaxp = 2*10*5; Xl = 20*log10(abs(X(1:kmaxp+1)));
plot([10*5+1,10*5+1],[-100,0],[0:kmaxp],max(Xl-max(Xl),-100)); grid;
xlabel('Frequency (Bins)'); ylabel('Magnitude (dB)');
title('b) Interpolated FFT of 10 Periods of Sinusoid');

Next Section:
Dynamic Range
Previous Section:
Properties of DB Scales