Real Exponents
The closest we can actually get to most real numbers is to compute a
rational number that is as close as we need. It can be shown that
rational numbers are dense in the real numbers; that is,
between every two real numbers there is a rational number, and between
every two rational numbers is a real number.3.1An irrational number can be defined as any real
number having a non-repeating decimal expansion. For example,
![]() is an irrational real number whose decimal expansion starts
out as3.2
is an irrational real number whose decimal expansion starts
out as3.2
![\begin{eqnarray*}
x &=& 0.\overline{123} \\ [5pt]
\quad\Rightarrow\quad 1000x &=...
...999x &=& 123\\ [5pt]
\quad\Rightarrow\quad x &=& \frac{123}{999}
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/mdft/img261.png)
Other examples of irrational numbers include
Their decimal expansions do not repeat.
Let
![]() denote the
denote the ![]() -digit decimal expansion of an arbitrary real
number
-digit decimal expansion of an arbitrary real
number ![]() . Then
. Then
![]() is a rational number (some integer over
is a rational number (some integer over ![]() ).
We can say
).
We can say
Since
![]() is defined for all
is defined for all ![]() , we naturally define
, we naturally define ![]() as the following mathematical limit:
as the following mathematical limit:
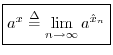
Next Section:
A First Look at Taylor Series
Previous Section:
Rational Exponents



















