Rational Exponents
A
rational
number is a real number that can be expressed as
a ratio of two finite integers:
Applying property (2) of exponents, we have
Thus, the only thing new is
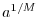
. Since
we see that
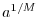
is the

th root of
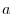
.
This is sometimes written
The

th root of a real (or complex) number is not unique. As we all
know, square roots give two values (
e.g.,
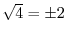
). In the
general case of

th roots, there are

distinct values, in
general. After proving
Euler's identity, it will be easy to find them
all (see §
3.11). As an example,
![$ \sqrt[4]{1}=1$](http://www.dsprelated.com/josimages_new/mdft/img252.png)
,
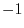
,

,
and
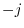
, since
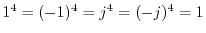
.
Next Section: Real ExponentsPrevious Section: Negative Exponents
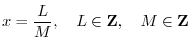
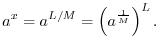
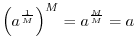
![$\displaystyle \zbox {a^{\frac{1}{M}} \isdef \sqrt[M]{a}.}
$](http://www.dsprelated.com/josimages_new/mdft/img250.png)
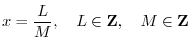
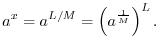
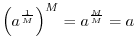
![$\displaystyle \zbox {a^{\frac{1}{M}} \isdef \sqrt[M]{a}.}
$](http://www.dsprelated.com/josimages_new/mdft/img250.png)