DSPRelated.com
Free Books
   Free Books    Mathematics of the DFT  

Signal/Vector Reconstruction from Projections

We now arrive finally at the main desired result for this section:


Theorem: The projections of any vector $ x\in{\bf C}^N$ onto any orthogonal basis set for $ {\bf C}^N$ can be summed to reconstruct $ x$ exactly.


Proof: Let $ \{\sv_0,\ldots,\sv_{N-1}\}$ denote any orthogonal basis set for $ {\bf C}^N$. Then since $ x$ is in the space spanned by these vectors, we have

$\displaystyle x= \alpha_0\sv_0 + \alpha_1\sv_1 + \cdots + \alpha_{N-1}\sv_{N-1} \protect$ (5.3)

for some (unique) scalars $ \alpha_0,\ldots,\alpha_{N-1}$. The projection of $ x$ onto $ \sv_k$ is equal to

$\displaystyle {\bf P}_{\sv_k}(x) = \alpha_0{\bf P}_{\sv_k}(\sv_0) + \alpha_1{\bf P}_{\sv_k}(\sv_1) + \cdots + \alpha_{N-1}{\bf P}_{\sv_k}(\sv_{N-1}) $

(using the linearity of the projection operator which follows from linearity of the inner product in its first argument). Since the basis vectors are orthogonal, the projection of $ \sv_l$ onto $ \sv_k$ is zero for $ l\neq k$:

$\displaystyle {\bf P}_{\sv_k}(\sv_l) \isdef \frac{\left<\sv_l,\sv_k\right>}{\l... ...ll} \underline{0}, & l\neq k \\ [5pt] \sv_k, & l=k. \\ \end{array} \right. $

We therefore obtain

$\displaystyle {\bf P}_{\sv_k}(x) = 0 + \cdots + 0 + \alpha_k{\bf P}_{\sv_k}(\sv_k) + 0 + \cdots + 0 = \alpha_k\sv_k. $

Therefore, the sum of projections onto the vectors $ \sv_k$, $ k=0,1,\ldots, N-1$, is just the linear combination of the $ \sv_k$ which forms $ x$:

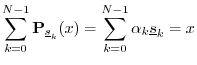
$\displaystyle \sum_{k=0}^{N-1} {\bf P}_{\sv_k}(x) = \sum_{k=0}^{N-1} \alpha_k \sv_k = x $

by Eq.$ \,$(5.3). $ \Box$

Next Section:
Gram-Schmidt Orthogonalization
Previous Section:
General Conditions