Free Books
   Free Books    Mathematics of the DFT  

The Sinc Function

Figure: The sinc function $ \protect$sinc$ (x) \protect\isdef \protect\sin(\pi x)/(\pi x)$.
\includegraphics[width=\twidth]{eps/Sinc}

The sinc function, or cardinal sine function, is the famous ``sine x over x'' curve, and is illustrated in Fig.D.2. For bandlimited interpolation of discrete-time signals, the ideal interpolation kernel is proportional to the sinc function

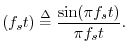
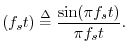
   sinc$\displaystyle (f_st) \isdef \frac{\sin(\pi f_st)}{\pi f_st}. $

where $ f_s$ denotes the sampling rate in samples-per-second (Hz), and $ t$ denotes time in seconds. Note that the sinc function has zeros at all the integers except 0, where it is 1. For precise scaling, the desired interpolation kernel is $ f_s$sinc$ (f_st)$, which has a algebraic area (time integral) that is independent of the sampling rate $ f_s$.

Next Section:
Reconstruction from Samples--The Math
Previous Section:
Reconstruction from Samples--Pictorial Version