DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Angular Motion in the Space-Fixed Frame

Let's now consider angular motion in the presence of linear motion of the center of mass. In general, we have [270]

$\displaystyle \underline{L}\eqsp \sum \underline{x}\times \underline{p} $

where the sum is over all mass particles in the rigid body, and $ \underline{p}$ denotes the vector linear momentum for each particle. That is, the angular momentum is given by the tangential component of the linear momentum times the associated moment arm. Using the chain rule for differentiation, we find

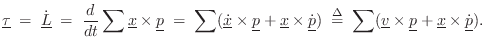
$\displaystyle \underline{\tau}\eqsp \dot{\underline{L}} \eqsp \frac{d}{dt}\sum ... ...m (\underline{v}\times\underline{p}+ \underline{x}\times \dot{\underline{p}}). $

However, $ \underline{v}\times \underline{p}=\underline{v}\times m\underline{v}=\underline{0}$, so that

$\displaystyle \underline{\tau}\eqsp \dot{\underline{L}} \eqsp \sum \underline{x}\times \dot{\underline{p}} \eqsp \sum \underline{x}\times \underline{f} $

which is the sum of moments of all external forces.

Next Section:
Euler's Equations for Rotations in the Body-Fixed Frame
Previous Section:
Body-Fixed and Space-Fixed Frames of Reference